It is an exercise that the space obtained by collapsing the boundary of 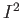 to a singleton is homeomorphic to
to a singleton is homeomorphic to 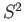 . Let
. Let 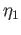 denote the quotient map
denote the quotient map
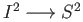 which collapses the boundary to a singleton and likewise let
which collapses the boundary to a singleton and likewise let
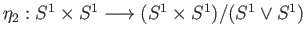 be the quotient map. The
map
be the quotient map. The
map
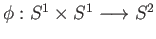 given by the prescription
given by the prescription
is well-defined and surjective.
Since 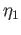 is continuous it follows that
is continuous it follows that  is continuous (why?). There is a unique bijective map
is continuous (why?). There is a unique bijective map
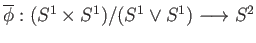 such that
such that
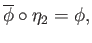 from which follows that
from which follows that
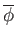 is continuous and a closed map since the domain is compact and the codomain
is
Hausdorff. Hence
is continuous and a closed map since the domain is compact and the codomain
is
Hausdorff. Hence
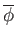 is a homeomorphism between
is a homeomorphism between
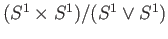 and
and 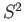 .
.
nisha
2012-03-20