- Prove the second equality in equation (41.1).
- Prove corollary (41.6).
- Prove that there is no injective continuous mapping from
 into
into
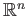 . ([11], p. 217)
. ([11], p. 217)
- Show that no proper subset of
 can be homeomorphic to
can be homeomorphic to  . ([11], p. 217)
. ([11], p. 217)
- Let
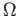 be an open subset of
be an open subset of
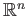 and
be an injective continuous map.
Show that
and
be an injective continuous map.
Show that  is a homeomorphism onto its image. ([11], p. 217)
is a homeomorphism onto its image. ([11], p. 217)
nisha
2012-03-20