Suppose that  is a topological space and
is a topological space and
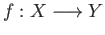 is a surjective mapping, let us consider the
various topologies on
is a surjective mapping, let us consider the
various topologies on  with respect to which
with respect to which  is continuous. Certainly the function
is continuous. Certainly the function  would be continuous if
would be continuous if  carries
the trivial topology where the only open sets are
carries
the trivial topology where the only open sets are 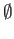 and
and  . The quotient topology on
. The quotient topology on  is the strongest topology
that makes
is the strongest topology
that makes  continuous. More explicitly consider the family
continuous. More explicitly consider the family
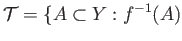
is open in
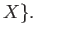
Since 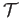 is closed under arbitrary unions, finite intersections and contains
is closed under arbitrary unions, finite intersections and contains  and the empty set,
we conclude that
and the empty set,
we conclude that 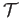 is a topology on
is a topology on  with respect to which
with respect to which  is continuous.
It is also clear that any strictly larger topology would render
is continuous.
It is also clear that any strictly larger topology would render  discontinuous.
discontinuous.
nisha
2012-03-20