- Prove that any continuous function
![$ f : [-1, 1] \longrightarrow [-1, 1]$](img235.png) has a fixed point, that is to say, there
exists a point
has a fixed point, that is to say, there
exists a point
![$ x \in [-1, 1]$](img236.png) such that
such that 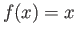 .
.
- Prove that the unit interval
![$ [0, 1]$](img13.png) is connected. Is it true that if
is connected. Is it true that if
![$ f : [0,1]\longrightarrow [0, 1]$](img159.png) has connected graph then
has connected graph then  is continuous? What if connectedness is replaced by path connectedness?
is continuous? What if connectedness is replaced by path connectedness?
- Suppose
 is a locally compact, non-compact, connected Hausdorff space, is its one point compactification connected?
What happens if
is a locally compact, non-compact, connected Hausdorff space, is its one point compactification connected?
What happens if  is already compact and Hausdorff?
is already compact and Hausdorff?
- Show that any connected metric space with more than one point must be uncountable.
Hint: Use Tietze's extension theorem and the fact that the connected sets in the real line are intervals.
- Show that the complement of a two dimensional linear subspace in
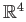 is connected. Hint: Denoting by
is connected. Hint: Denoting by
 be the two
dimensional vector space, show that
be the two
dimensional vector space, show that
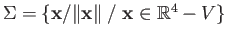 is connected
using stereographic projection or otherwise.
is connected
using stereographic projection or otherwise.
- How many connected components are there in the complement of the cone
in
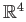 ? Hint: The complement of this cone is filled up by families of hyperboloids. Examine if there is
a connected set
? Hint: The complement of this cone is filled up by families of hyperboloids. Examine if there is
a connected set 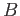 meeting each member of a given family.
meeting each member of a given family.
- A map
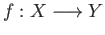 is said to be a local homeomorphism if for
is said to be a local homeomorphism if for 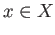 there exist neighborhoods
there exist neighborhoods
 of
of 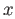 and
and  of
of 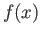 such that
such that
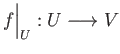 is a homeomorphism. If
is a homeomorphism. If
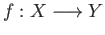 is a local homeomorphism and a proper map, then for each
is a local homeomorphism and a proper map, then for each
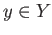 ,
, 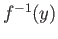 is a finite set. Show that the map
is a finite set. Show that the map
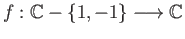 given by
given by
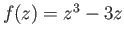 is a local homeomorphism. Is it a proper map?
is a local homeomorphism. Is it a proper map?
#4968#>
nisha
2012-03-20
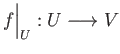 is a homeomorphism. If
is a homeomorphism. If