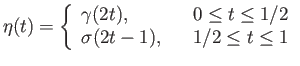Let 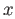 and
and 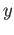 be arbitrary points of
be arbitrary points of  and let
and let  be the set of all points of
be the set of all points of  that can be joined to
that can be joined to 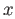 by a path. Clearly
by a path. Clearly  is non-empty since it contains the point
is non-empty since it contains the point 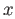 . If
we show that
. If
we show that  is open and closed then by connectedness of
is open and closed then by connectedness of  it would follow that
it would follow that  would equal the whole space
would equal the whole space
 . In particular
. In particular  contains
contains 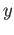 thereby proving that there is a path in
thereby proving that there is a path in  joining
joining 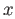 and
and 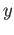 . First we show that
. First we show that  is open. Well, let
is open. Well, let 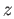 be an arbitrary point of
be an arbitrary point of  and choose a path
and choose a path
![$ \gamma :[0, 1] \longrightarrow X$](img218.png) such that
such that
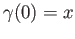 and
and
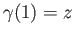 . Choose a path connected neighborhood
. Choose a path connected neighborhood 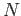 of
of 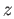 and
and 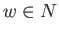 be arbitrary.
Then there is a path
be arbitrary.
Then there is a path  lying in
lying in 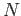 joining
joining 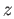 and
and 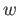 . We now juxtapose
. We now juxtapose  and
and  by defining
by defining
![$ \eta :[0, 1]\longrightarrow X$](img225.png) as
as
By virtue of the gluing lemma 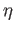 is continuous and defines a path joining
is continuous and defines a path joining 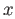 and
and 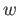 . Hence
. Hence 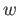 belongs to
belongs to
 and so
and so
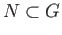 . We now show that
. We now show that  is closed as well. Let
is closed as well. Let
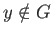 and
and 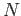 be a path connected
neighborhood of
be a path connected
neighborhood of 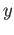 . Then we show that
. Then we show that
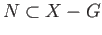 . Well, if not, pick
. Well, if not, pick
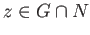 and there is a path
and there is a path  in
in  joining
joining 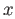 and
and 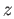 and a path
and a path  in
in 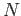 joining
joining 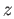 and
and 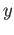 . Juxtaposing we would get a path in
. Juxtaposing we would get a path in  joining
joining 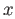 and
and 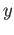 which would contradict the fact that
which would contradict the fact that
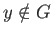 . So
. So 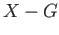 is also open in
is also open in  and the proof is complete.
nisha
2012-03-20
and the proof is complete.
nisha
2012-03-20