(i) Choose a Lebesgue number for the open cover
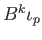 . According to theorem (34.3), the images of the simplicies occurring in
the chain
. According to theorem (34.3), the images of the simplicies occurring in
the chain
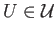 are the same as the images under
are the same as the images under  of the affine simplicies occurring in
of the affine simplicies occurring in
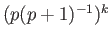 , where
, where 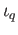 is the identity map of
is the identity map of 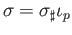 . However, theorem (34.4) states that the simplicies
occurring in
. However, theorem (34.4) states that the simplicies
occurring in
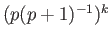 have diameters less than
have diameters less than
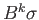 . Thus, if we choose
. Thus, if we choose
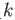 sufficiently large the image of each of the simplicies in
sufficiently large the image of each of the simplicies in 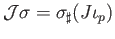 would lie in one of the open sets of
would lie in one of the open sets of
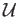 .
.
To prove (ii) we use the naturality of 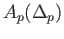 and proceed as in the proof of theorem (34.4).
Let
and proceed as in the proof of theorem (34.4).
Let
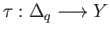 have its image in
have its image in
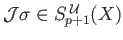 . Then
. Then
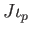 . But we see immediately from the definition of
. But we see immediately from the definition of 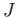 in theorem (34.3) that
in theorem (34.3) that
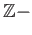 is a
is a
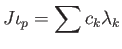 linear combination:
linear combination:
where each 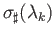 is a (degenerate) affine (p+1) simplex contained in
is a (degenerate) affine (p+1) simplex contained in 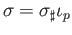 and hence
and hence
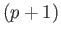 is a singular
is a singular 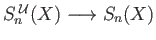 simplex with image contained in
simplex with image contained in  .
. 
nisha
2012-03-20
![]() and proceed as in the proof of theorem (34.4).
Let
and proceed as in the proof of theorem (34.4).
Let
![]() have its image in
have its image in
![]() . Then
. Then
![]() . But we see immediately from the definition of
. But we see immediately from the definition of ![]() in theorem (34.3) that
in theorem (34.3) that
![]() is a
is a
![]() linear combination:
linear combination: