Given points
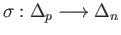 in
the standard
in
the standard  simplex
simplex  , the continuous map
, the continuous map
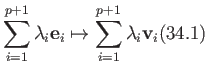 given in terms of the barycentric coordinates
given in terms of the barycentric coordinates
is called an affine 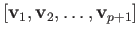 simplex and is denoted by
simplex and is denoted by
![$ [{\bf v}_1, {\bf v}_2,\dots, {\bf v}_{p+1}]$](img2591.png) .
Note that the given need not be affinely independent.
Each such
.
Note that the given need not be affinely independent.
Each such  is an element of
is an element of
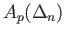 and the subgroup generated by them is called the
group of affine
and the subgroup generated by them is called the
group of affine 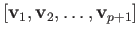 simplicies in
simplicies in 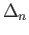 denoted by
denoted by
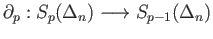 . Thus
. Thus
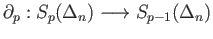 is the set of all formal linear combinations with integer coefficients of affine simplicies. Since the face maps (29.1)
are affine maps we conclude from exercise 2 that the boundary homomorphism
is the set of all formal linear combinations with integer coefficients of affine simplicies. Since the face maps (29.1)
are affine maps we conclude from exercise 2 that the boundary homomorphism
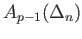 maps
maps
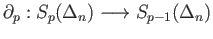 into
into
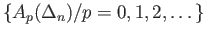 and so we get a subcomplex
and so we get a subcomplex
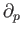 with boundary maps as the restrictions of
with boundary maps as the restrictions of
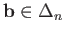 to
to
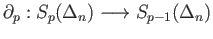 .
.
If
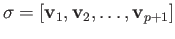 is a given point the cone over the affine simplex
is a given point the cone over the affine simplex
![$ \sigma = [{\bf v}_1, {\bf v}_2,\dots, {\bf v}_{p+1}]$](img2599.png) with vertex apex
with vertex apex
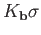 is denoted by
is denoted by
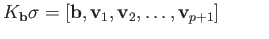 and is defined as
and is defined as
The cone
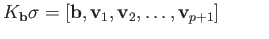 is thus an affine
is thus an affine 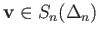 simplex. If we start with a zero simplex namely, a point
simplex. If we start with a zero simplex namely, a point
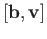 , the cone over it is the line segment
, the cone over it is the line segment
![$ [{\bf b}, {\bf v}]$](img2605.png) .
Since
.
Since
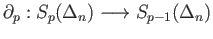 is a free abelian group generated
by the affine
is a free abelian group generated
by the affine  simplicies, we obtain by extension a group homomorphism
simplicies, we obtain by extension a group homomorphism
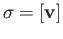 . As in the proof of theorem (29.7) it is easy to
compute the boundary of the cone
. As in the proof of theorem (29.7) it is easy to
compute the boundary of the cone
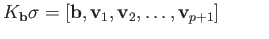 for any affine
for any affine  simplex.
simplex.
For a zero simplex
![$ \sigma = [{\bf v}]$](img2607.png) we evidently have
we evidently have
![$ \partial _1K_{\bf b}(\sigma) = \sigma - [{\bf b}]$](img2608.png) . We now calculate the faces of the affine
. We now calculate the faces of the affine 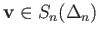 simplex
simplex
 . If
. If 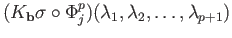 ,
,
This is the cone over the 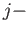 th face of
th face of
![$ [{\bf v}_1, {\bf v}_2,\dots, {\bf v}_{p+1}]$](img2591.png) .
Turning to the case
.
Turning to the case 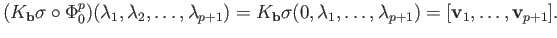 ,
,
Using equation (29.4) we immediately get the following result.
nisha
2012-03-20
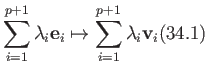 given in terms of the barycentric coordinates
given in terms of the barycentric coordinates
![]() is a given point the cone over the affine simplex
is a given point the cone over the affine simplex
![]() with vertex apex
with vertex apex
![]() is denoted by
is denoted by
![]() and is defined as
and is defined as
![]() we evidently have
we evidently have
![]() . We now calculate the faces of the affine
. We now calculate the faces of the affine ![]() simplex
simplex
![]() . If
. If ![]() ,
,