Assume  is path connected but not connected. Then there is a non constant continuous function
is path connected but not connected. Then there is a non constant continuous function
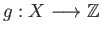 say
say 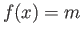 and
and 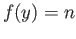 for a pair of distinct integers
for a pair of distinct integers 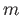 and
and  .
But there is also a continuous function
.
But there is also a continuous function
![$ f : [0. 1] \longrightarrow X$](img209.png) such that
such that 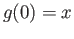 and
and 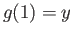 .
The composite function
.
The composite function
![$ f\circ g : [0, 1] \longrightarrow \mathbb{Z}$](img212.png) is non constant which is a contradiction.
is non constant which is a contradiction.
nisha
2012-03-20