The theorem can be used to prove that the sphere
is connected. Define 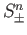 to be the closed upper and lower hemispheres. Then
to be the closed upper and lower hemispheres. Then 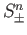 are connected.
The intersection of these hemispheres is
are connected.
The intersection of these hemispheres is
 . One can now apply induction observing first that the circle
. One can now apply induction observing first that the circle 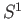 is connected since it is the continuous
image of the real line under the map
is connected since it is the continuous
image of the real line under the map
nisha
2012-03-20