- Prove that a topological space is compact if and only if it satisfies the following condition known as the
finite intersection property. For every family
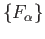 of closed sets with
of closed sets with
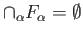 ,
there is a finite sub-collection whose intersection is empty
,
there is a finite sub-collection whose intersection is empty
- Show that
![$ f : [0,1]\longrightarrow [0, 1]$](img159.png) is continuous if and only if its graph is a
compact subset of
is continuous if and only if its graph is a
compact subset of 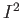 .
.
- Examine whether the exponential map from
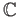 onto
onto
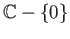 is proper. What about the exponential
map as a map from
is proper. What about the exponential
map as a map from
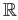 onto
onto
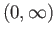 ?
?
- (Gluing Lemma)
Suppose that
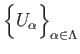 is a family of open subsets of a topological space and
for each
is a family of open subsets of a topological space and
for each
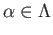 we are given a continuous function
we are given a continuous function
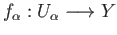 . Assume that whenever
. Assume that whenever
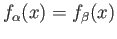 whenever
whenever
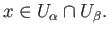 Show that there exists a unique continuous function
Show that there exists a unique continuous function
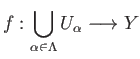 such that
such that
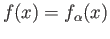 for all
for all
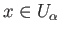 and for all
and for all
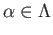 .
Show that the result holds if all the
.
Show that the result holds if all the
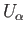 are closed sets and
are closed sets and 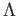 is a finite set.
is a finite set.
- How would you show rigorously that the closed unit disc in the plane
is homeomorphic to the closed
triangular region determined by three
non-collinear points? You are allowed to use
results from complex analysis, provided you state them clearly.
- Prove that any two closed triangular planar regions (as described in the previous exercise)
are homeomorphic. Show that any such closed triangular region is homeomorphic to
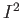 .
.
- Suppose that
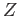 is a Hausdorff space and
is a Hausdorff space and
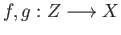 are continuous functions then the set
are continuous functions then the set
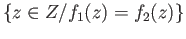 is closed in
is closed in 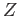 .
.
- Show that the space obtained by rotating the circle
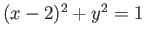 about the
about the 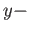 axis is homeomorphic to
axis is homeomorphic to
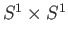 .
.
#4965#>
nisha
2012-03-20
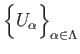 is a family of open subsets of a topological space and
for each
is a family of open subsets of a topological space and
for each
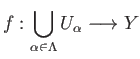 such that
such that