Note that if 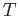 is non-singular, it is a proper map and so it extends continuously as a map
of
is non-singular, it is a proper map and so it extends continuously as a map
of  sending the point at infinity to itself. Conversely, if
sending the point at infinity to itself. Conversely, if 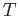 fails to be bijective then there is a sequence of
points
fails to be bijective then there is a sequence of
points 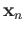 such that
such that
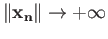 but
but
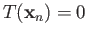 for every
for every  . Thus if
. Thus if 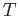 were to
extend continuously as a map of
were to
extend continuously as a map of  we would be forced to map the point at infinity namely the north pole to
(the point of
we would be forced to map the point at infinity namely the north pole to
(the point of  corresponding to) the origin. On the other hand since
corresponding to) the origin. On the other hand since 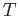 is not the zero map, pick a
vector
is not the zero map, pick a
vector 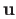 such that
such that
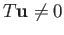 and the sequence
and the sequence 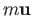 converges (as
converges (as
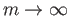 )
to the point at infinity on
)
to the point at infinity on  . Thus by continuity we would have
. Thus by continuity we would have
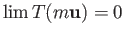 , as
, as
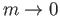 .
Hence,
.
Hence,
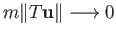 which is plainly false since
which is plainly false since
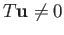 .
.
More important examples are furnished by regarding 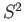 as the one point compactification of the plane
as the one point compactification of the plane
 and using the field structure on the plane. The proof of the following is an exercise.
and using the field structure on the plane. The proof of the following is an exercise.
nisha
2012-03-20
![]() as the one point compactification of the plane
as the one point compactification of the plane
![]() and using the field structure on the plane. The proof of the following is an exercise.
and using the field structure on the plane. The proof of the following is an exercise.