Consider the sphere
and the plane
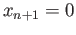 of the equator. Let
of the equator. Let
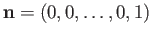 and
and 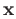 be a general point on the equatorial plane. The line through
be a general point on the equatorial plane. The line through 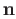 and
and 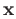 is described parametrically by
is described parametrically by
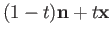 and meets the sphere at points corresponding to the roots of the quadratic equation
and meets the sphere at points corresponding to the roots of the quadratic equation
The root 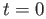 corresponds to the point
corresponds to the point 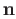 and the second root
and the second root
is continuous with respect to 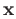 and provides a point
and provides a point
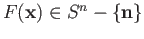 .
The map
.
The map 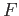 is a bijective continuous map
between the plane
is a bijective continuous map
between the plane
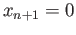 and
and
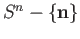 . Note that the origin is mapped to the
south pole by
. Note that the origin is mapped to the
south pole by 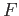 .
The inverse map
.
The inverse map  is called the stereographic projection. Let us now show that
is called the stereographic projection. Let us now show that  is also continuous
whereby it follows that
is also continuous
whereby it follows that 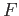 is a homeomorphism.
is a homeomorphism.
Well, let 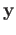 be a point on the sphere minus the north pole
be a point on the sphere minus the north pole 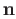 . The ray emanating from
. The ray emanating from 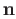 and
passing through
and
passing through 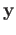 meets the plane at the point
meets the plane at the point
We see that  is also continuous and so the sphere minus its north pole is homeomorphic to
is also continuous and so the sphere minus its north pole is homeomorphic to
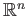 .
.
It is useful to note that the stereographic projection takes points 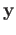 close to the north pole to points
close to the north pole to points
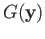 of
of
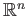 such that
such that
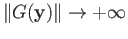 .
We summarize the discussion as a theorem.
.
We summarize the discussion as a theorem.
nisha
2012-03-20
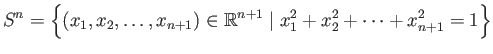
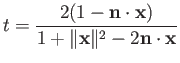
![]() be a point on the sphere minus the north pole
be a point on the sphere minus the north pole ![]() . The ray emanating from
. The ray emanating from ![]() and
passing through
and
passing through ![]() meets the plane at the point
meets the plane at the point
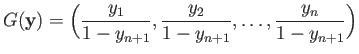
![]() close to the north pole to points
close to the north pole to points
![]() of
of
![]() such that
such that
![]() .
We summarize the discussion as a theorem.
.
We summarize the discussion as a theorem.