We begin with the observation that the condition spelled out in (i) is independent of the choice of  and also independent of the choice of
and also independent of the choice of
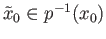 . Well, changing the element
. Well, changing the element
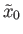 in the fiber would give a conjugate
subgroup but the normality hypothesis
says that the conjugacy class of the subgroup
in the fiber would give a conjugate
subgroup but the normality hypothesis
says that the conjugacy class of the subgroup
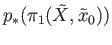 is a singleton.
Second, a group isomorphism must take a normal subgroup to a normal subgroup and so the condition (i) does not depend on the choice of
the base point
is a singleton.
Second, a group isomorphism must take a normal subgroup to a normal subgroup and so the condition (i) does not depend on the choice of
the base point  .
.
Proof that (i) implies (ii). Suppose that
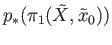 is a normal subgroup of
is a normal subgroup of
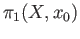 and
and  is an arbitrary loop in
is an arbitrary loop in  based at
based at  . Let
. Let
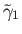 and
and
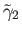 be two lifts of
be two lifts of  with initial points
with initial points
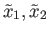 such that
such that
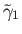 a closed loop. Then
a closed loop. Then
which means ![$ [\gamma]$](img28.png) is in the stabilizer of
is in the stabilizer of
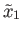 and hence, by (iii) of theorem (17.2),
and hence, by (iii) of theorem (17.2),
![$ [\gamma]$](img28.png) belongs to the stabilizer of
belongs to the stabilizer of
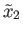 . Thus
. Thus
and we see that
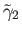 is also closed.
is also closed.
Proof that (ii) implies (i). If
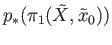 is not a normal subgroup of
is not a normal subgroup of
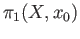 then it
has at least two distinct conjugates which,
by virtue of theorem (17.2),
must be the stabilizers of say
then it
has at least two distinct conjugates which,
by virtue of theorem (17.2),
must be the stabilizers of say
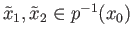 .
Thus there exists
.
Thus there exists
![$ [\gamma] \in p_*(\pi_1({\tilde X}, {\tilde x}_1)) = \;$](img1441.png) Stab
Stab
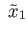 but
but
![$ [\gamma] \notin p_*(\pi_1({\tilde X}, {\tilde x}_2)) = \;$](img1443.png) Stab
Stab
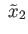 . In other words
. In other words
where
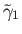 and
and
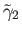 are the lifts of
are the lifts of  starting at
starting at
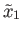 and
and
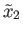 respectively. Thus
the lift
respectively. Thus
the lift
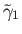 of
of  is closed whereas the lift
is closed whereas the lift
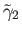 is not closed.
nisha
2012-03-20
is not closed.
nisha
2012-03-20
![]() is a normal subgroup of
is a normal subgroup of
![]() and
and ![]() is an arbitrary loop in
is an arbitrary loop in ![]() based at
based at ![]() . Let
. Let
![]() and
and
![]() be two lifts of
be two lifts of ![]() with initial points
with initial points
![]() such that
such that
![]() a closed loop. Then
a closed loop. Then
![]() is not a normal subgroup of
is not a normal subgroup of
![]() then it
has at least two distinct conjugates which,
by virtue of theorem (17.2),
must be the stabilizers of say
then it
has at least two distinct conjugates which,
by virtue of theorem (17.2),
must be the stabilizers of say
![]() .
Thus there exists
.
Thus there exists
![]() Stab
Stab
![]() but
but
![]() Stab
Stab
![]() . In other words
. In other words