Statement (iv) follows from (ii). Assertion (iii) is a general fact about transitive group actions.
To prove that the group action is transitive, let
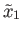 and
and
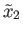 be two points in the fiber
be two points in the fiber
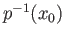 and
and
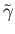 be a path in
be a path in
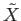 joining
joining
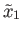 and
and
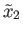 . The image path
. The image path
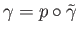 is then a loop
in
is then a loop
in  based at
based at  and so represents an element of
and so represents an element of
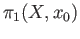 .
Also
.
Also
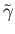 being the lift of
being the lift of  starting at
starting at
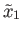 ,
we see that
,
we see that
Turning now to the proof of (ii), let
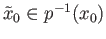 and
and  be an arbitrary loop in
be an arbitrary loop in  based at
based at  .
Then
.
Then ![$ [\gamma]$](img28.png) belongs to the stabilizer of
belongs to the stabilizer of
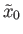 if and only if its lift starting at
if and only if its lift starting at
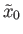 terminates at the same point
terminates at the same point
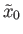 . That is
if and only if
. That is
if and only if  lifts as a loop based at
lifts as a loop based at
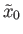 . But this
is equivalent to saying
. But this
is equivalent to saying
![$ [{\tilde \gamma}] \in \pi_1({\tilde X}, {\tilde x}_0)$](img1430.png) and
and
![$ \gamma = p_*[{\tilde \gamma}]$](img1431.png) .
Conversely if
.
Conversely if
![$ [\gamma] \in \pi_1(X,x_0)$](img570.png) is
the image under
is
the image under 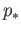 of
of
![$ [\tilde \gamma] \in \pi_1({\tilde X}, {\tilde x}_0)$](img1433.png) then
then
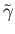 is a loop homotopic to a lift of
is a loop homotopic to a lift of  starting at
starting at
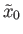 .
But any two such lifts have the same terminal point which means
.
But any two such lifts have the same terminal point which means
That is to say ![$ [\gamma]$](img28.png) belongs to the stabilizer of
belongs to the stabilizer of
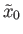 and that completes the proof.
nisha
2012-03-20
and that completes the proof.
nisha
2012-03-20