We first show that the action is well-defined. That is to say if 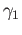 and
and 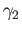 are homotopic loops based
at
are homotopic loops based
at  then for
then for
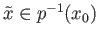
where
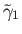 and
and
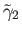 are lifts of
are lifts of 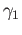 and
and 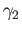 starting at
starting at
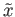 . Well, if
. Well, if 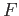 is the homotopy between
is the homotopy between
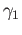 and
and 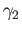 then
then 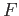 has a unique lift
has a unique lift
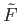 satisfying
satisfying
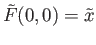 .
In other words,
.
In other words,
![$ {\tilde F}: [0, 1]\times [0, 1]\longrightarrow {\tilde X}$](img1332.png) is the unique continuous map such that
is the unique continuous map such that
In particular the image set
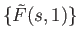 as
as 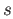 runs through
runs through ![$ [0, 1]$](img13.png) , must be a connected subset of
, must be a connected subset of
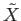 . But since
. But since 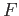 is
a homotopy of loops based at
is
a homotopy of loops based at  ,
,
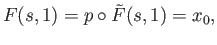
for all
![$\displaystyle s \in [0, 1].$](img1127.png)
Hence
![$ \{{\tilde F}(s, 1)/ s\in [0, 1]\} \subset p^{-1}(x_0)$](img1412.png) which means
which means
![$ \{{\tilde F}(s, 1)/ s\in [0, 1]\}$](img1413.png) is a singleton since
is a singleton since
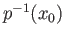 is discrete. In particular,
is discrete. In particular,
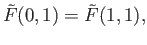
that is,
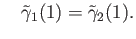
Next, we show that (15.1) defines a right group action. First
let us note that if
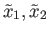 and
and
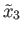 are three points in
are three points in
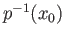 and
and
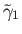 and
and
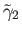 is a pair of paths joining
is a pair of paths joining
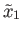 to
to
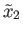 and
and
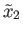 to
to
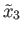 respectively then
respectively then
Now let 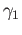 and
and 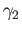 be two loops in
be two loops in  based at
based at  . Assume that
. Assume that
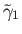 is the unique lift of
is the unique lift of
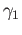 starting at
starting at
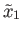 and
and
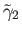 is the unique lift of
is the unique lift of 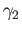 starting at the point
starting at the point
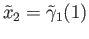 then the juxtaposition
then the juxtaposition
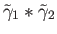 is defined and
is the unique lift of
is defined and
is the unique lift of
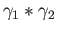 starting at
starting at
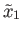 . Thus,
. Thus,
On the other hand,
Note that if we had tried to operate from the left we would instead get an anti-action. This is one of the instances where it is
important to have the book-keeping done correctly from the very outset.
Finally the constant loop
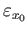 at
at  lifts as the constant loop starting at
lifts as the constant loop starting at
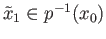 and so (17.1) implies
and so (17.1) implies
We now examine the issues related to this group action namely,
its transitivity and the stabilizer subgroups of various
points of
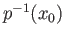 .
.
nisha
2012-03-20
![]() and
and
![]() are three points in
are three points in
![]() and
and
![]() and
and
![]() is a pair of paths joining
is a pair of paths joining
![]() to
to
![]() and
and
![]() to
to
![]() respectively then
respectively then
![]() at
at ![]() lifts as the constant loop starting at
lifts as the constant loop starting at
![]() and so (17.1) implies
and so (17.1) implies
![]() .
.