Let  be a locally compact, non-compact Hausdorff space and
be a locally compact, non-compact Hausdorff space and
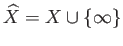 be the one point union of
be the one point union of  with an additional point
with an additional point 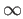 .
The topology
.
The topology 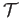 consists of all the open subsets in
consists of all the open subsets in  as well as all the subsets of the form
as well as all the subsets of the form
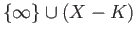 ,
where
,
where  ranges over all the compact subsets of
ranges over all the compact subsets of  . The following theorem summarizes the properties of
. The following theorem summarizes the properties of
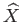 and the proof is left for the reader.
and the proof is left for the reader.
nisha
2012-03-20