The student is advised to draw relevant pictures as he reads on.
Suppose that a cover
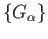 has no Lebesgue number. Then for every
has no Lebesgue number. Then for every
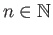 ,
,
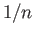 is not a Lebesgue number and so there is a point
is not a Lebesgue number and so there is a point 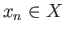 such that the ball of radius
such that the ball of radius 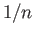 centered at
centered at 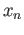 is not contained in any of the open sets in the covering. By compactness the sequence
is not contained in any of the open sets in the covering. By compactness the sequence 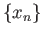 has a
convergent subsequence converging to a point
has a
convergent subsequence converging to a point 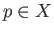 . Choose an
. Choose an 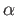 such that
such that
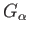 contains
contains  and there is a
and there is a
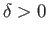 such that the ball of radius
such that the ball of radius 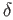 around
around  is contained in
is contained in
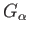 .
Now take
.
Now take  large enough that
large enough that
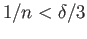 and
and
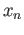 is contained in the ball of radius
is contained in the ball of radius 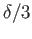 centered at
centered at  .
.
Now, since the ball of radius 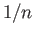 with center
with center 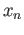 is not contained in any of the open sets in our covering, there exists
is not contained in any of the open sets in our covering, there exists 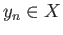 such that
such that
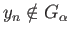 and
and
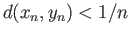 . But
. But
So 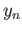 is in the ball of radius
is in the ball of radius 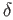 centered at
centered at  and so
and so
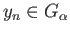 which is a contradiction.
nisha
2012-03-20
which is a contradiction.
nisha
2012-03-20
![]() with center
with center ![]() is not contained in any of the open sets in our covering, there exists
is not contained in any of the open sets in our covering, there exists ![]() such that
such that
![]() and
and
![]() . But
. But