A subset of
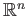 is compact (with respect to the subspace topology)
if and only if it is closed and bounded.
is compact (with respect to the subspace topology)
if and only if it is closed and bounded.
The theorem provides a profusion of examples of compact spaces.
- The unit sphere
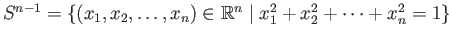 is compact.
is compact.
- The unit square
![$ I^2 = [0, 1]\times [0,1]$](img77.png) is compact.
is compact.
- The set of all
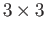 matrices is clearly homeomorphic to
matrices is clearly homeomorphic to
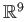 .
Then the set of all
.
Then the set of all 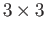 orthogonal matrices, denoted by
orthogonal matrices, denoted by
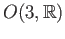 is
is compact. That is to say the orthogonal group is compact. The result readily generalizes to the group of
is
is compact. That is to say the orthogonal group is compact. The result readily generalizes to the group of
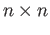 orthogonal matrices.
orthogonal matrices.
- Think of the set of all
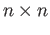 matrices with complex entries as
matrices with complex entries as
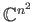 which in turn may be viewed
as
which in turn may be viewed
as
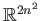 . The set of all
. The set of all 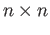 unitary matrices is then easily seen to be
a compact space. These matrices form a group known as the unitary group
unitary matrices is then easily seen to be
a compact space. These matrices form a group known as the unitary group 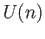 .
.
- The set of all
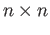 unitary matrices with determinant one is also a closed bounded subset of
unitary matrices with determinant one is also a closed bounded subset of
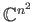 and so is compact. This is the special unitary group
and so is compact. This is the special unitary group 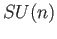 .
.
nisha
2012-03-20