-
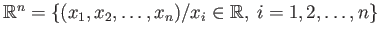
-
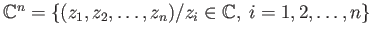
-
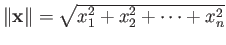 ,
,
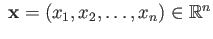
-
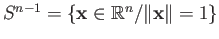
-
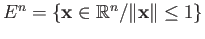
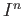 is the standard unit cube, the Cartesian product of
is the standard unit cube, the Cartesian product of 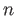 copies of
copies of ![$ [0, 1]$](img13.png) .
.
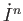 is the (topological) boundary of
is the (topological) boundary of 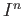 .
.
-
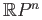 is the
is the 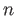 -dimensional real projective space
-dimensional real projective space
-
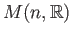 is the set of all
is the set of all 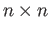 matrices with real entries
matrices with real entries
-
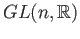 is the set of all invertible
is the set of all invertible 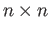 matrices with real entries
matrices with real entries
-
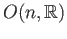 is the set of all orthogonal matrices with real entries
is the set of all orthogonal matrices with real entries
-
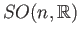 is the set of all orthogonal matrices with real entries and determinant one
is the set of all orthogonal matrices with real entries and determinant one
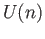 is the set of all
is the set of all 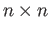 unitary matrices with complex entries
unitary matrices with complex entries
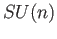 is the set of all
is the set of all 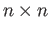 unitary matrices with determinant one
unitary matrices with determinant one
- Gr is the category of groups
- AbGr is the category of abelian groups
- Top is the category of topological spaces
-
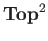 is the category of pairs of topological spaces
is the category of pairs of topological spaces
-
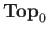 is the category of pointed topological spaces
is the category of pointed topological spaces
nisha
2012-03-20