| |
Waiting time distribution
Now let us consider the distribution function of 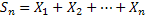 , which is the waiting time for the occurrence of , which is the waiting time for the occurrence of 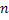 number of events (which is deterministic) in a probabilistic time frame, say number of events (which is deterministic) in a probabilistic time frame, say 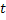 . .
Now the 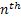 events occurs prior or at time events occurs prior or at time 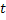 iff the number of events occurring by time iff the number of events occurring by time 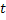 is at least is at least 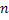 , i.e., the following holds true, i.e., , i.e., the following holds true, i.e.,
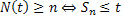
Thus
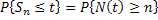
i.e., 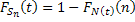 , where , where 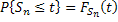 and and 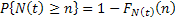
Thus:
Thus:
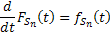
which implies 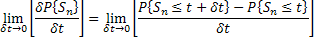
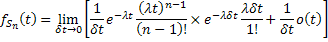
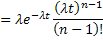
Using the fact that 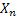 , , 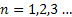 are i.i.d exponential random variables with mean are i.i.d exponential random variables with mean 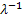 we show we show 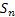 has gamma distribution with has gamma distribution with 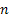 and and 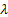 as the parameters, hence the probability density function is of the form as the parameters, hence the probability density function is of the form 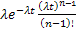 . .
Note
- Remember that the exponential distributed discussed here is also referred to as the gamma distribution wit h parameters
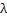 and 1. and 1.
- From the reproduction property of gamma distribution one notes that if
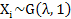 , then , then 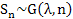 . .
|