Interarrival time distribution
For a Poisson process let us denote 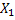 as the time for the occurrence of the 1st event, i.e., the time between the occurrence between the 1st and the as the time for the occurrence of the 1st event, i.e., the time between the occurrence between the 1st and the 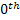 event. Extending this notion we have event. Extending this notion we have 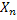 as the time between the occurrence the as the time between the occurrence the 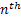 and and 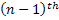 event. Then this sequence event. Then this sequence 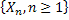 is what we call as the the sequence of interarrival times. is what we call as the the sequence of interarrival times.
As an illustration one can refer to Figure 2.6, which points out the fact that the occurrence of the 1st, 2nd, 3rd,…. events (i.e., event number) are fixed, but when each of the individual event would occur is not known to us and hence the time interval between two consecutive occurrences of events say 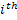 and and 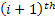 is stochastic. is stochastic.
Figure 2.6: Illustration of interarrival time which is stochastic
|