| |
For 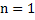 we have we have
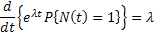 |
(using (2.1)) |
| i.e., |
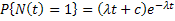 |
But 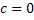 as as 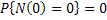 , hence: , hence:
Using mathematical induction we have:
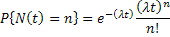
In general 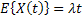 , ,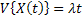 and both are not independent of and both are not independent of 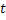 . This type of process can be said to be an evolutionary process, thus Poisson process is not a stationary process but rather an evolutionary process. . This type of process can be said to be an evolutionary process, thus Poisson process is not a stationary process but rather an evolutionary process.
It is important to understand that 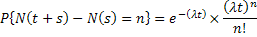 , and it gives us the same meaning when we assume , and it gives us the same meaning when we assume 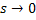 . Another important fact worth mentioning is that a Poisson process is a Markov Process with the transition probability being independent of the past. . Another important fact worth mentioning is that a Poisson process is a Markov Process with the transition probability being independent of the past.
|