Derivation of Poisson Process
Let us define 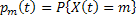 , which means that , which means that 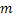 events occur in time events occur in time 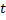 . .
Now 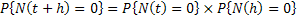 , means the probability of the number of events in the time frame , means the probability of the number of events in the time frame 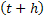 being zero is equal to the product of the probabilities that the number of events occurring in time frame being zero is equal to the product of the probabilities that the number of events occurring in time frame 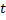 and and 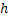 each is zero. This is true as the property of independent increments holds true for the counting process and the Poisson process we consider here. each is zero. This is true as the property of independent increments holds true for the counting process and the Poisson process we consider here.
In the conceptual sense this time 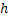 is taken to be infinitesimally small, i.e., is taken to be infinitesimally small, i.e.,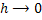 (Figure 2.4). (Figure 2.4).
Figure 2.4: The concept of time h as it becomes zero
Hence
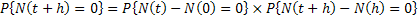
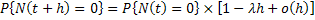
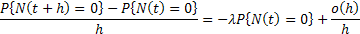
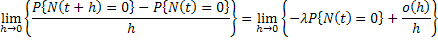
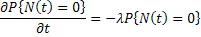
Solving this using simple integration furnishes us with  , where , where 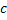 is the constant of integration is the constant of integration |