| |
Solution Methodology
Reliability search algorithms are characterized by the use of analytical techniques to find a particular point (Most Probable Point (MPP) of failure) in the feasible space which can be related to the probability of the system failure, defined by the limit state. The solution methodology proceeds as follows. We first transform the input vector 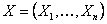 into the standard normal space into the standard normal space 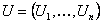 , where , where 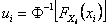 , , 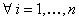 , and Φ-1 is the inverse of the normal distribution function. This transformation maintains the distribution functions being identical in both X and U space respectively. Thus the MPP, now in U space, is the minimum distance point from the constraint boundary , and Φ-1 is the inverse of the normal distribution function. This transformation maintains the distribution functions being identical in both X and U space respectively. Thus the MPP, now in U space, is the minimum distance point from the constraint boundary 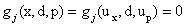 to the origin, and this minimum distance is to the origin, and this minimum distance is 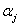 . .
Now in an inverse reliability problem, the required reliability 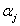 is given, and the percentile performance corresponding to is given, and the percentile performance corresponding to 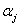 is to be evaluated, such that one needs to defined βj (reliability index), which is given by is to be evaluated, such that one needs to defined βj (reliability index), which is given by 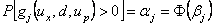 . Thus the MPP becomes the tangent point of a hyper sphere in the U space with the radius βj and the contour of gj(ux, d, up), such that at MPP one achieves optimality. The type of optimization, i.e., maximization (minimization) achieved at MPP depends on which part of the tail of the distribution MPP corresponds to, and as such the right (left) position of MPP signifies that one achieves maximization (minimization) at those points respectively. So for (12.5) we consider the MPP corresponding to the left tail. Likewise for the maximization problem, when we have the objective function as maximum of . Thus the MPP becomes the tangent point of a hyper sphere in the U space with the radius βj and the contour of gj(ux, d, up), such that at MPP one achieves optimality. The type of optimization, i.e., maximization (minimization) achieved at MPP depends on which part of the tail of the distribution MPP corresponds to, and as such the right (left) position of MPP signifies that one achieves maximization (minimization) at those points respectively. So for (12.5) we consider the MPP corresponding to the left tail. Likewise for the maximization problem, when we have the objective function as maximum of  , we formulated it accordingly and solve it to obtain the MPP. , we formulated it accordingly and solve it to obtain the MPP.
|