| |
Use of Eigen values and eigen vectors to calculate higher transition probabilities
Suppose you have a Markov chain with 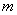 states, where states, where 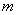 is finite, and it is also given that the transition probability matrix is is finite, and it is also given that the transition probability matrix is 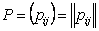 , then one can very easily calculate the , then one can very easily calculate the 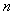 step transition probability matrix, step transition probability matrix, 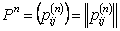 , such that we utilize the equation, , such that we utilize the equation, 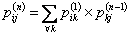 , , 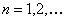 , where , where 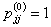 and and 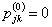 for for 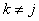 . Now our main intention of this discussion is to utilize the concept of eigen values and eigen vectors to calculate . Now our main intention of this discussion is to utilize the concept of eigen values and eigen vectors to calculate 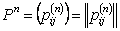 . .
One must remember that for a square matrix, 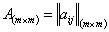 , the characteristics roots of the equation: , the characteristics roots of the equation:  , where , where 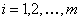 are called the eigen values, and they are given by are called the eigen values, and they are given by 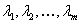 . While . While 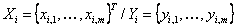 , , 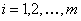 , is the right/left eigen vector, corresponding to , is the right/left eigen vector, corresponding to 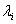 , , 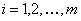 , such that the following equation (for , such that the following equation (for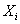 ), s, i.e., ), s, i.e., 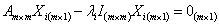 , , 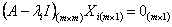 , i.e., , i.e.,
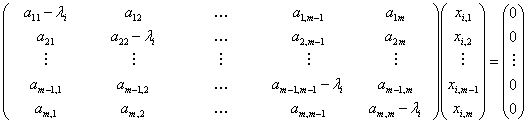 holds for holds for 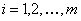 , such that we will finally obtain , such that we will finally obtain 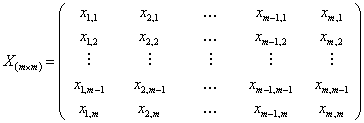 , where the , where the 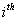 column corresponds to the eigen vector corresponding to the column corresponds to the eigen vector corresponding to the 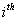 characteristics root, characteristics root, 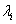 . .
|