Application of Markov chain in trying to judge the efficiency of algorithms in OR
In certain OR problems the idea is to search and determine the best amongst a set of 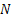 number of search points so that at each point we find the objective function and try to ascertain whether we are able to reach our optimum (whether minimum or maximum that is a different question). Now consider that in a linear programming problem (LPP) if we have number of search points so that at each point we find the objective function and try to ascertain whether we are able to reach our optimum (whether minimum or maximum that is a different question). Now consider that in a linear programming problem (LPP) if we have 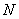 number of corner points, then we have to search number of corner points, then we have to search 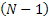 number of search points. number of search points.
Let us illustrate that with a simple example.
Example 12.1
A paint company manufactures two different types of paints, P1 and P2, from the raw materials, M1 and M2. The following table provides the basic data for our example
|
Tons of raw materials per ton of |
Maximum daily availability (tons)
|
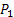
|
|
Raw material M1 |
6 |
4 |
24 |
Raw material M2 |
1 |
2 |
6 |
Profit per ton (Rs. 1000) |
5 |
4 |
|
A marketing survey indicates that the daily demand for 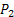 cannot exceed that of cannot exceed that of 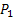 by more than 1 ton. Also the maximum daily demand of by more than 1 ton. Also the maximum daily demand of 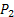 is 2 tons. The company would like to determine the optimal mix of the two paints in order to maximize its daily profit. is 2 tons. The company would like to determine the optimal mix of the two paints in order to maximize its daily profit.
Step1: To determine the amount to be produced of
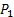 and and
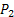 we denote we denote 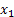 as the amount of as the amount of
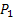 paint and paint and 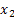 as the amount of as the amount of
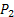 paint. paint.
Step 2: To construct the objective function the company wants to increase its profit as much as possible. If we denote the profit function as z, then we need to maximize 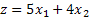 . .
Step 3: The constraints, that restricts the raw materials and demand, is related by the fundamental principle that 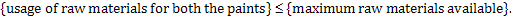 |