| |
If one wants to analyze brand loyalty using the concept of Markov Chain model, then the number of states very naturally becomes equal to 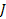 , as we are only interested in studying the long term transition probabilities of a particular person in our study group switching from one brand say the , as we are only interested in studying the long term transition probabilities of a particular person in our study group switching from one brand say the 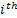 to another one say the to another one say the 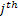 in the group of in the group of 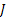 , where , where 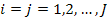 in any combination, i.e., one can move from in any combination, i.e., one can move from 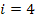 to to 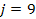 , or from , or from 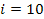 to to 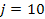 , etc. Hence theoretically one may consider that after the survey the transition probability matrix between the , etc. Hence theoretically one may consider that after the survey the transition probability matrix between the 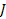 number of brands may be noted down as given below: number of brands may be noted down as given below:
Table 11.1 : Transition probability matrix for the brand loyalty example
|
1 |
2 |
. |
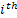
|
. |
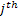
|
. |
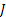
|
1 |
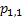
|
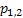
|
. |
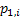
|
. |
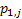
|
. |
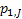
|
2 |
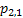
|
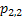
|
. |
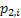
|
. |
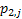
|
. |
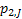
|
. |
. |
. |
. |
. |
. |
. |
. |
. |
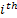
|
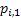
|
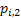
|
. |
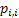
|
. |
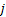
|
. |
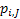
|
. |
. |
. |
. |
. |
. |
. |
. |
. |
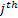
|
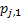
|
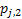
|
. |
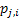
|
. |
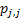
|
. |
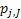
|
. |
. |
. |
. |
. |
. |
. |
. |
. |
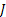
|
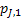
|
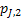
|
. |
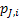
|
. |
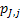
|
. |
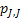
|
Now if we denote this matrix as 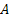 , our aim is to study , our aim is to study 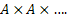 in the long run such that as a brand manager of a particular product in a company can analyze the trend of switching between brands of a group of customer in order to draw some meaningful conclusion in the long run. in the long run such that as a brand manager of a particular product in a company can analyze the trend of switching between brands of a group of customer in order to draw some meaningful conclusion in the long run.
In order to find 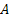 , things like income effect, age, quality, availability, image, etc., can be brought in to the study which throw some light on the how these variables have a positive/negative impact on brand switching and how one can find the respective probability as given above. The way to analyze that can be through the questionnaire made which would give us a good picture about how to modify and quantify the probabilities of transition between brands in the short term, which can be further analyzed to find the long term probabilities such that brand loyalty as a objective value can be studied more intensely and in detail. , things like income effect, age, quality, availability, image, etc., can be brought in to the study which throw some light on the how these variables have a positive/negative impact on brand switching and how one can find the respective probability as given above. The way to analyze that can be through the questionnaire made which would give us a good picture about how to modify and quantify the probabilities of transition between brands in the short term, which can be further analyzed to find the long term probabilities such that brand loyalty as a objective value can be studied more intensely and in detail.
|