Profit maximization considering partial backlogging
Let us assume the case when each unit of demand results in a revenue of 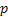 , while each lost sales is backlogged with probability , while each lost sales is backlogged with probability 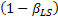 , where , where 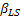 is the probability of lost sales. One should remember that each lost sales results in a loss of unit revenue of value is the probability of lost sales. One should remember that each lost sales results in a loss of unit revenue of value 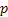 and an additional unit cost of and an additional unit cost of 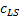 which may be due to loss of good will. Finally which may be due to loss of good will. Finally 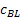 is the unit cost due to special ordering which is due to loss of good will and as such the main focus then is to expedite the order in order to regain back the good will lost. is the unit cost due to special ordering which is due to loss of good will and as such the main focus then is to expedite the order in order to regain back the good will lost.
Now considering both expected revenue and expected cost, one can find out the expected profit/loss which is given by the formulae given below in (9.1)
Example for backorder cases
The system under consideration is such that one is interested to find the optimal order quantiy, 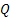 , at some reorder point , at some reorder point 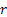 . Few relevant assumptions for the model are: . Few relevant assumptions for the model are:
- Unit cost of the item is
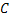 , which is constant and is independent of , which is constant and is independent of 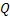 . .
- The per unit back ordered cost is
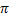 . .
- Maximum number of order outstanding is 1.
- Cost for operating the information system in order to study the production process is independent of either
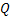 or or 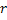 . .
For a better understanding of this order model one can refer to Figure 9.2, where orders are made at 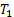 , , 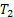 , etc. time periods and the order level is , etc. time periods and the order level is 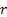 . Now considering the safety stock is . Now considering the safety stock is 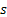 , then the average on hand inventory is given by , then the average on hand inventory is given by  . .
If procurement lead time, 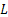 , is constant then the safety stock level is given by , is constant then the safety stock level is given by 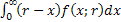 . But in case lead time is stochastic with a probability distribution of . But in case lead time is stochastic with a probability distribution of 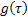 , then the safety stock value is calculated as , then the safety stock value is calculated as 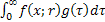 . .
In case 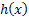 represents the marginal distribution of lead time demand, and in case we consider that to be normally distributed then the annual variable cost represents the marginal distribution of lead time demand, and in case we consider that to be normally distributed then the annual variable cost 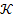 is given by the following expression (9.2). is given by the following expression (9.2).
where:
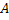 = Cost of placing an order = Cost of placing an order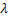 = Average annual demand = Average annual demand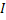 = Inventory carrying cost = Inventory carrying cost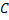 = Unit cost of the item = Unit cost of the item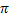 = Per unit back order cost = Per unit back order cost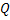 = Optimal order quantity = Optimal order quantity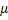 = Expected value of demand distribution, which is denoted by = Expected value of demand distribution, which is denoted by 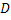 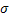 = Standard deviation of demand distribution, which is denoted by = Standard deviation of demand distribution, which is denoted by 
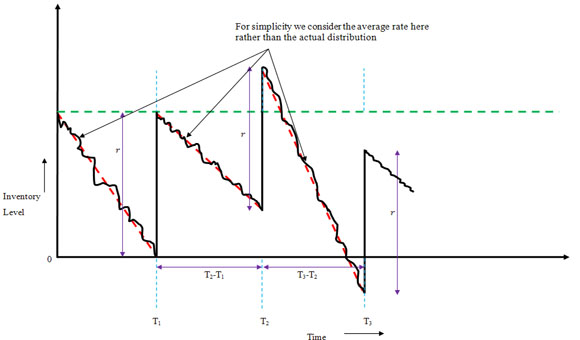
Figure 9.2: The  system system
|