Definition : the Markov chain is irreducible if the equivalence reduces only to one class i.e., all state communicate.
One dimension random walks
In one dimension random walk our variable is defined as 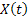 , where the realized values are scalars only and are defined as , where the realized values are scalars only and are defined as 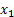 , , 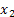 ,…., ,…., 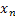 ,……. Let us illustrate this with a simple example. Consider you toss an unbiased coin repeatedly. Then Figure 6.8 shows how the random walk movement takes place in the one dimension case considering the actual occurrences are either a head (H) or a tail (T). Moreover one can define the outcomes occurring after each toss as a stage and the collection of all different occurrences at any stage as states. Thus I, II, III, and so on represents the stages while the outcomes in each stage is the corresponding states of that stage, ,……. Let us illustrate this with a simple example. Consider you toss an unbiased coin repeatedly. Then Figure 6.8 shows how the random walk movement takes place in the one dimension case considering the actual occurrences are either a head (H) or a tail (T). Moreover one can define the outcomes occurring after each toss as a stage and the collection of all different occurrences at any stage as states. Thus I, II, III, and so on represents the stages while the outcomes in each stage is the corresponding states of that stage,
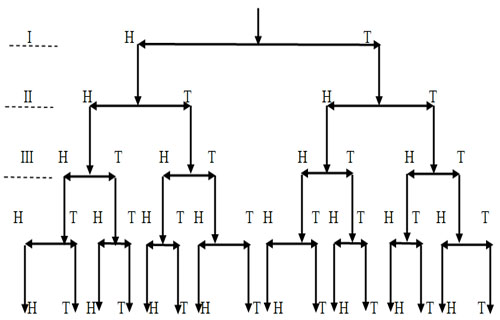
Figure 6.8: One dimension random walk with the example where you toss a coin
One should note that the Central Limit Theorem (CLT) describes the important aspects of the behavious of the simple random walk (in one dimension).
|