Martingales
1. Suppose 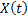 is a real values state space in either discrete or continuous time. Then is a real values state space in either discrete or continuous time. Then 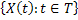 is a martingale iff is a martingale iff
a. 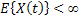 , , 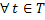
b. 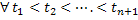
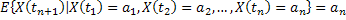 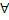 a, t a, t
Martingle talks of expected value and states that the expected value in finite.
2.  is a Markov Process iff is a Markov Process iff 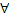 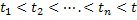 for which for which
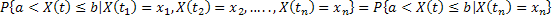 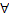 x, t. One must remember that a and b are arbitrary. x, t. One must remember that a and b are arbitrary.
Markov Process talks about distribution function : Hence the concept of a Martingle states that the expected value of future depends only on present. While the Markov process states that the distribution function of future depends only on the present.
Let 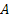 be an interval of the real line, then be an interval of the real line, then 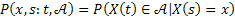 , , 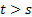 is called the transition probability function. Diagrammatically we can denote this in Figure 6.7 is called the transition probability function. Diagrammatically we can denote this in Figure 6.7

Figure 6.7: Diagrammatic representation of transition probability function
|