Example 6.1
Pick a non-trivial 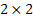 and and 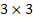 matrices and calculate matrices and calculate 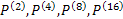 , etc. On can also attempt to find, , etc. On can also attempt to find, 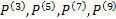 , etc. , etc.
Consider an arbitrary but fixed state 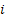 . For that define . For that define 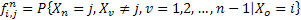 ; ;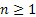 . .
Then 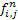 is the probability (given we are in state is the probability (given we are in state 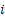 at time at time 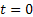 ), of the first attainment of state ), of the first attainment of state 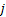 occuring at the occuring at the 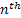 transition, which may be called the first passage time. transition, which may be called the first passage time.
By definition we have 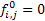 , , 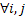 and and 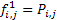 , then one can claim that: , then one can claim that:
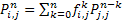 , where , where 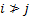 , , 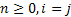 , , 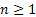 . .
Diagrammatically it can be shown in Figure 6.3.
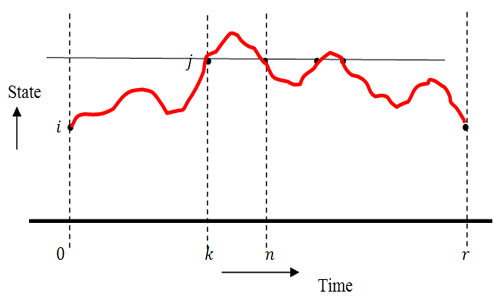
Figure 6.3: A simple stochastic process
Contrast this with the first order Markov chain.
|