Example 5.2
Let us consider another example of renewal theory, where we discuss the problem relate to arrival of customers in a grocer shop or departmental store. Let us consider the grocer store has 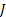 number of different items on display and amongst these number of different items on display and amongst these 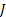 number of items the customer chooses his/her product(s). Let the inter-arrival times of customers have a distribution, number of items the customer chooses his/her product(s). Let the inter-arrival times of customers have a distribution, 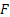 . Furthermore one can safely assume that the amounts desired of any product amongst . Furthermore one can safely assume that the amounts desired of any product amongst 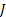 is independent, and the distribution is is independent, and the distribution is 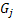 , , 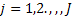 . The store uses the . The store uses the 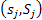 ordering policy, which means if the level of stock for the ordering policy, which means if the level of stock for the 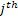 item falls below item falls below 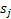 , then the inventory of the same is brought back to , then the inventory of the same is brought back to 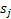 and that is done instantaneously (which is practically not possible, yet we assume this for simplicity). and that is done instantaneously (which is practically not possible, yet we assume this for simplicity).
Thus the inventory level after serving the customer if be denoted by 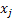 then we have: then we have:
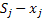 if if 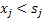
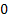 if if 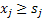
In case if we denote 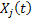 as the inventory level for the as the inventory level for the 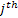 item at time item at time 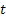 , then our main concern is to find , then our main concern is to find 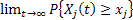 which is given by which is given by 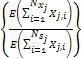 , where , where
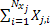 = Amount of time in the cycle when the inventory is not ordered. = Amount of time in the cycle when the inventory is not ordered.
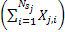 = Amount of total time of the cycle. = Amount of total time of the cycle.
Example 5.3
As a third example suppose a sophisticated machine consists of 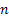 crucial parts/components which function independently (even though this is not valid, yet we take this assumption to be true for our example). Each part of the machine has an exponential alternating renewal process in which it fluctuates by going up and down (like a switch with ON and OFF positions) for which the averages times are crucial parts/components which function independently (even though this is not valid, yet we take this assumption to be true for our example). Each part of the machine has an exponential alternating renewal process in which it fluctuates by going up and down (like a switch with ON and OFF positions) for which the averages times are 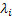 and and 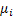 . The sophisticated machine is said to function if at least one of the . The sophisticated machine is said to function if at least one of the 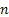 component is in ON position. Let us also denote by component is in ON position. Let us also denote by 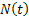 the number of time the sophisticated machine breaks down in the time interval of the number of time the sophisticated machine breaks down in the time interval of 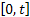 . .
Then the aim of the shop floor manager is to calculate the mean time between breakdowns of this sophisticated machine. In order to calculate this, he/she will try to find out the probability of breakdown in the time interval of 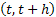 , where , where 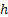 is very small. A simple concept using which we can find this value is to first consider the case when only one part/component is functioning and the rest is very small. A simple concept using which we can find this value is to first consider the case when only one part/component is functioning and the rest 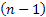 are down and then after that have all the parts/components fail. Using calculations we can show that the value is given by are down and then after that have all the parts/components fail. Using calculations we can show that the value is given by 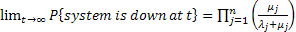 . . |