| |
Simulation study using Gamma distribution: Next assume
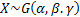 , i.e., the gamma distribution, where , i.e., the gamma distribution, where
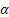 , ,
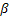 and and
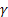 as the shape, scale and location parameters respectively. For simplicity assume as the shape, scale and location parameters respectively. For simplicity assume
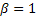 , ,
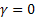 , then one can easily see that , then one can easily see that 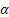 =E(X), for which the best estimate is =E(X), for which the best estimate is 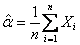 . Considering the bounded SEL and LINEX risk problem for the gamma distribution the corresponding optimal sample sizes, are respectively given by . Considering the bounded SEL and LINEX risk problem for the gamma distribution the corresponding optimal sample sizes, are respectively given by 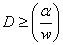 and and 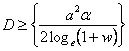 (with (with 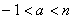 ). Thus with unknown ). Thus with unknown 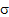 one may solve both these bounded risk problems using any one of the sequential analysis methods discussed earlier. one may solve both these bounded risk problems using any one of the sequential analysis methods discussed earlier.
Simulation study using Extreme Value Distribution: Finally consider
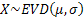 as the Extreme Value Distribution (EVD) with m as its location parameter and s as the scale parameter. We know the estimate of as the Extreme Value Distribution (EVD) with m as its location parameter and s as the scale parameter. We know the estimate of 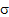 is is 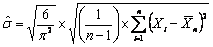 , where , where 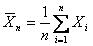 , while that of , while that of
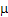 is is 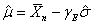 . Hence the SEL bounded risk optimal sample size is . Hence the SEL bounded risk optimal sample size is 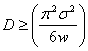 . In case one considers the LINEX loss function, then the optimal sample size for the bounded LINEX loss risk is . In case one considers the LINEX loss function, then the optimal sample size for the bounded LINEX loss risk is 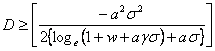 , when , when 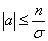 and and 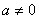 . Hence to find the optimal estimate of . Hence to find the optimal estimate of 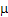 , with unknown s, both these bounded risk problems may be solved employing any one of the sequential sampling methods discussed. Furthermore this estimate of , with unknown s, both these bounded risk problems may be solved employing any one of the sequential sampling methods discussed. Furthermore this estimate of 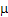 may be used to calculate E(X). Hence one first finds the bounded risk estimate of may be used to calculate E(X). Hence one first finds the bounded risk estimate of 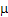 and then calculates E(X) using and then calculates E(X) using 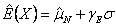 , where , where 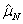 , is the estimate of , is the estimate of 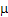 found using any one of the sequential sampling plans. found using any one of the sequential sampling plans.
|