Step # 2
Define another renewal process 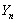 , , 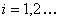 and fix a constant and fix a constant 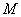 , such that we have , such that we have
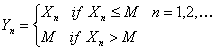
Let 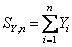 and and 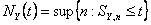 . Now if . Now if 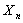 is the inter arrival time, then by definition is the inter arrival time, then by definition 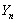 is also inter arrival time, but which has been truncated by the value of is also inter arrival time, but which has been truncated by the value of 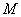 , such that , such that 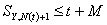 , i.e., , i.e.,
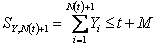 . .
For 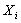 and and 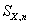
For 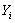 and and 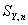
Thus from 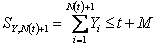 we have we have 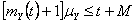 , hence , hence 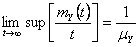 . .
Now as 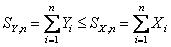 and it would immediately follow that and it would immediately follow that 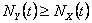 and and 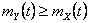 , hence , hence 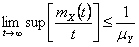 and as and as 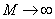 , then , then 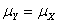 , thus we have , thus we have 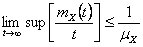 . .
Hence using 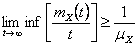 and and 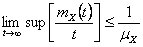 we immediately have we immediately have 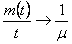 as as
Remember in the sequential problem we are always interested to find the average value of 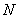 , i.e., as per the first order asymptotic property we should have , i.e., as per the first order asymptotic property we should have 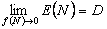 or else more generally and strongly we should have the second order asymptotic property as or else more generally and strongly we should have the second order asymptotic property as 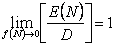 . .
|