Example 4.9
Suppose 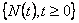 be a renewal process and suppose that for all be a renewal process and suppose that for all 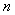 and and 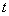 , conditional on the event that , conditional on the event that 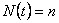 , the events , the events 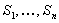 are distributed as the order statistics of a set of independent uniform are distributed as the order statistics of a set of independent uniform 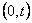 random variables. Then we can easily prove that random variables. Then we can easily prove that 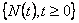 is a Poisson process. is a Poisson process.
For few more concepts of renewal theory and to dwell further into the concept of stopping time for the renewal process, let us consider 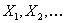 as the inter arrival time of a renewal process. Now for this renewal process we should stop the first renewal after as the inter arrival time of a renewal process. Now for this renewal process we should stop the first renewal after 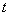 , i.e., at the , i.e., at the 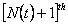 renewal. What we need to verify is the fact that renewal. What we need to verify is the fact that 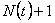 is indeed a stopping time for this sequence is indeed a stopping time for this sequence 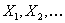 , i.e., , i.e., 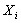 , , 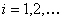
Note
Notice I have made an emphasis on the word a. This is due to the fact that depending on what is needed to be found, the stopping time will vary. Like if you are interested to find the mean for say a general distribution, 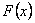 , then the concept and the values of stopping time for find the mode will not be same as the former case when one is interested to find the mean. , then the concept and the values of stopping time for find the mode will not be same as the former case when one is interested to find the mean.
Again continuing with our problem we have
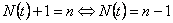
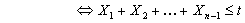 , i.e., , i.e., 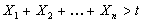
Now see that the event 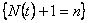 depends on depends on 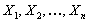 and definitely not on and definitely not on 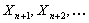 , hence obviously , hence obviously 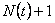 is a stopping time which depends on is a stopping time which depends on 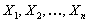 and definitely not on and definitely not on  . From Wald's equation we know that when . From Wald's equation we know that when 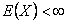 we would have we would have 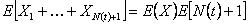
Thus the following corollary is true, which is
Corollary 4.6
If 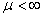 , then , then 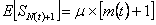
|