Definition
A renewal or a counting process nomenclature by 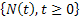 is a non-negative stochastic process which denotes the occurrences of an event (this is what we were discussing in the above four examples) during the time interval is a non-negative stochastic process which denotes the occurrences of an event (this is what we were discussing in the above four examples) during the time interval 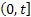 where the time duration between consecutive events are where the time duration between consecutive events are
(i) positive, (ii) independent and (iii) identically distributed random variables, i.e., i.i.d. r.v.
Let 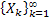 denote the successive occurence times of components which are counted (number denote the successive occurence times of components which are counted (number 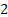 in Example # 4.1 or the refrigerators for which you are willing to give free service facilities in Example # 4.2 or the components which you may replace in case of failure or in case of general replacement schedule which you have planned for the machine in Example # 4.3 or in Example # 4.4 where you replace the electric bulb the moment the earlier one stops working), and successively placed into service, such that in Example # 4.1 or the refrigerators for which you are willing to give free service facilities in Example # 4.2 or the components which you may replace in case of failure or in case of general replacement schedule which you have planned for the machine in Example # 4.3 or in Example # 4.4 where you replace the electric bulb the moment the earlier one stops working), and successively placed into service, such that 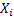 is the elapsed time from the occurrence of the is the elapsed time from the occurrence of the 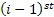 event until the occurrence of the event until the occurrence of the 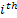 event. event.
Then we can write 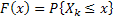 for for 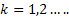 which will denote the common probability distribution of which will denote the common probability distribution of 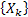 . A quick look at the probability distribution will make it obvious that the following is true, which is . A quick look at the probability distribution will make it obvious that the following is true, which is 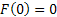 , and it signifies that , and it signifies that 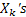 are positive random variable. are positive random variable.
Now let us define 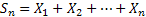 for for 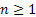 and it is also obvious from simple logic and convention that and it is also obvious from simple logic and convention that 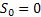 . Moreover . Moreover 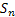 is the waiting time (total waiting time) until the occurrence of the is the waiting time (total waiting time) until the occurrence of the 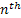 event. Note event. Note 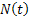 is equal to the number of indices is equal to the number of indices 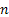 for which for which 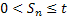 , hence we depict the situation using Figure 4.1. , hence we depict the situation using Figure 4.1.
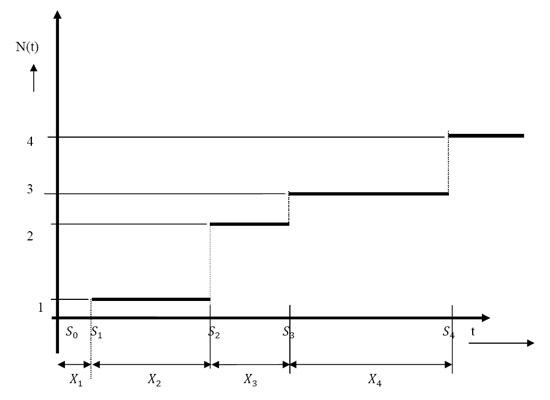
Figure 4.1: Simple concept of renewal process using diagrammatic illustration
Note
Thus if one considers Figure 4.1 then we have (i) 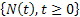 as the counting process, while (ii) as the counting process, while (ii) 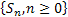 as the partial sum process. Thus (i) or (ii) interchangeable is called the renewal process. as the partial sum process. Thus (i) or (ii) interchangeable is called the renewal process.
|