Oscillations in s Two Area System

Consider the simple power system shown in Fig. 9.11 in which two machines are operating. Let us assume that starting with the initial angles δ₁ and δ₂ with respect to some reference at nominal frequency, machine 1 accelerates while machine 2 decelerates from this nominal frequency. We then have

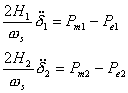(9.25)

where the subscripts 1 and 2 refer to machines 1 and 2 respectively. Let us assume that the transmission line is loss less. Then in the simple case where the power from machine 1 flows to machine 2, we get

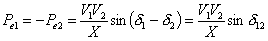(9.26)

where δ₁₂ = δ₁ - δ₂ .

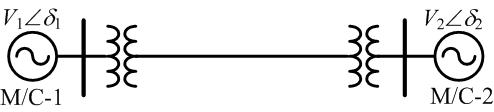
Fig. 9.11 Single-line diagram of a two-machine power system.

Now since the system is lossless, (9.26) will also imply that P_m1 = - P_m2 . This means that in the steady state, the power generated at machine 1 is absorbed through machine 2. Combining (9.25) and (9.26) we get

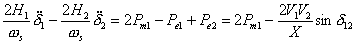(9.27)

Let us now assume that H₁ = H₂ = H , V₁ = V₂ = 1.0 per unit and P_m1 = 0. We then get from (9.27)

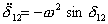(9.28)

where the oscillation frequency ω is given by

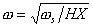(9.29)

Thus the weighted difference of angles will approximate simple harmonic motion for small changes in δ₁₂ and the frequency will decrease for an increase in inertia H or impedance X . Another aspect can be seen by adding the system to give

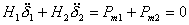(9.30)

Thus the overall acceleration of the machine group will depend on the overall balance between power generated and consumed. Usually there are governors on the generators to reduce generated power if the system frequency increases.