Symmetrical Component Transformation

Before we discuss the symmetrical component transformation, let us first define the α -operator. This has been given in (1.34) and is reproduced below.

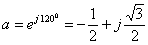(7.1)

Note that for the above operator the following relations hold

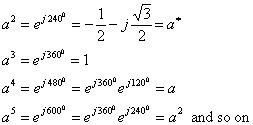(7.2)

Also note that we have

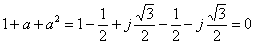(7.3)

Using the a -operator we can write from Fig. 7.1 (b)

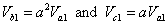(7.4)

Similarly from Fig. 7.1 (c) we get

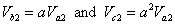(7.5)

Finally from Fig. 7.1 (d) we get

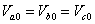(7.6)

	(7.7)
	(7.8)
	(7.9)

Therefore,

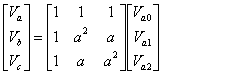(7.10)

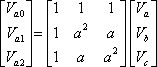(7.11)

The symmetrical component transformation matrix is then given by

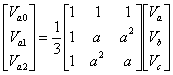(7.12)

Defining the vectors V _a012 and V _abc as

we can write (7.4) as

where C is the symmetrical component transformation matrix and is given by

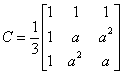(7.13)

The original phasor components can be obtained from the inverse symmetrical component transformation, i.e.,

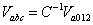(7.14)

Finally, if we define a set of unbalanced current phasors as I_abc and their symmetrical components as I_a012 , we can then define

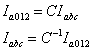(7.15)

Example 7.1

Example 7.2