Section IV:  Thevenin Impedance And Z_bus Matrix

To establish relationships between the elements of the Z_bus matrix and Thevenin equivalent, let us consider the following example.

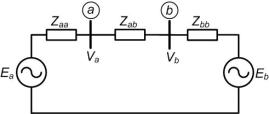
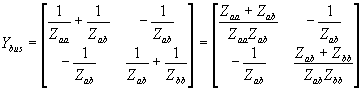
Example 3.4 Consider the two bus power system shown in Fig. 3.15. It can be seen that the open-circuit voltages of buses a and b are Va and Vb respectively. From (3.11) we can write the Ybus matrix of the system as Fig. 3.15 Two-bus power system of Example 3.4. The determinant of the above matrix is     Therefore the Zbus matrix is       Solving the last two equations we get 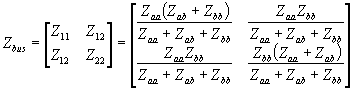(3.50)       Now consider the system of Fig. 3.15. The Thevenin impedance of looking into the system at bus- a is the parallel combination of Zaa and Zab + Zbb, i.e., 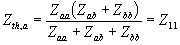(3.51)     Similarly the Thevenin impedance obtained by looking into the system at bus- b is the parallel combination of Zbb and Zaa + Zab, i.e., 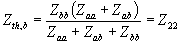(3.52)     Hence the driving point impedances of the two buses are their Thevenin impedances. Let us now consider the Thevenin impedance while looking at the system between the buses a and b . From Fig. 3.15 it is evident that this Thevenin impedance is the parallel combination of Zab and Zaa + Zbb, i.e.,     With the values given in (3.50) we can write       Comparing the last two equations we can write 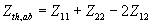(3.53)

As we have seen in the above example in the relation V = Z_bus I , the node or bus voltages V_i, i = 1, ... , n are the open circuit voltages. Let us assume that the currents injected in buses 1, ... , k - 1 and k + 1, ... , n are zero when a short circuit occurs at bus k . Then Thevenin impedance at bus k is

(3.54)

From (3.51), (3.52) and (3.54) we can surmise that the driving point impedance at each bus is the Thevenin impedance.

Let us now find the Thevenin impedance between two buses j and k of a power system. Let the open circuit voltages be defined by the voltage vector V° and corresponding currents be defined by I° such that

(3.55)

Now suppose the currents are changed by ΔI such that the voltages are changed by ΔV . Then

(3.56)

Comparing (3.55) and (3.56) we can write

(3.57)

Let us now assume that additional currents ΔI_k and ΔI_k are injected at the buses k and j respectively while the currents injected at the other buses remain the same. Then from (3.57) we can write

(3.58)

We can therefore write the following two equations form (3.58)

The above two equations can be rewritten as

	(3.59)
	(3.60)

Since Z_jk = Z_kj the network can be drawn as shown in Fig. 3.16. By inspection we can see that the open circuit voltage between the buses k and j is

(3.61)

and the short circuit current through these two buses is

(3.62)

Also during the short circuit V_k- V_j = 0. Therefore combining (3.59) and (3.60) we get

(3.63)

Combining (3.61) to (3.63) we find the Thevenin impedance between the buses k and j as

(3.64)

The above equation agrees with our earlier derivation of the two bus network given in (3.53).

Fig 3.16  Thevenin equivalent between buses k and j