Power in a Lossless Line
The power flow through a lossless line can be given by the mid point voltage and current equations given in (2.66) and (2.67). Since the power factor at this point is unity, real power over the line is given by
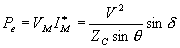 |
(2.71) |
If V = V0 , the rated voltage, we can rewrite the above expression in terms of the natural power as
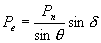 |
(2.72) |
For a short transmission line we have
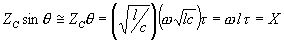 |
(2.73) |
where X is the total reactance of the line. Equation (2.71) then can be modified to obtain the well known power transfer relation for the short line approximation as
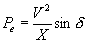 |
(2.74) |
In general it is not necessary for the magnitudes of the sending and receiving end voltages to be same. The power transfer relation given in (2.72) will not be valid in that case. To derive a general expression for power transfer, we assume
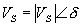 and and 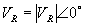 |
|
If the receiving end real and reactive powers are denoted by PR and QR respectively, we can write from (2.52)
Equating real and imaginary parts of the above equation we get
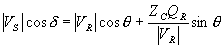 |
(2.75) |
and
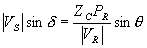 |
(2.76) |
Rearranging (2.76) we get the power flow equation for a losslees line as
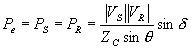 |
(2.77) |
To derive expressions for the reactive powers, we rearrange (2.75) to obtain the reactive power delivered to the receiving end as
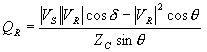 |
(2.78) |
Again from equation (2.61) we can write
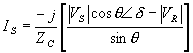 |
(2.79) |
The sending end apparent power is then given by
Equating the imaginary parts of the above equation we get the following expression for the reactive generated by the source
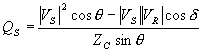 |
(2.80) |
The reactive power absorbed by the line is then
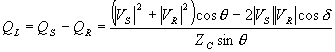 |
(2.81) |
It is important to note that if the magnitude of the voltage at the two ends is equal, i.e., ½VS½ = ½VR½ = V, the reactive powers at the two ends become negative of each other, i.e., QS = QR . The net reactive power absorbed by the line then becomes twice the sending end reactive power, i.e., QL = 2QS . Furthermore, since cosθ ≈ 1 for small values of θ, the reactive powers at the two ends for a short transmission line are given by
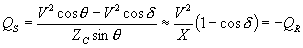 |
(2.82) |
The reactive power absorbed by the line under this condition is given by
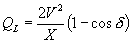 |
(2.83) |
|