Impact of Series Compensator on Voltage Profile

In the equivalent schematic diagram of a series compensated power system is shown in Fig. 10.10, the receiving end current is equal to the sending end current, i.e., I_S = I_R . The series voltage V_Q is injected in such a way that the magnitude of the injected voltage is made proportional to that of the line current. Furthermore, the phase of the voltage is forced to be in quadrature with the line current. We then have

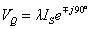(10.20)

The ratio λ/X is called the compensation level and is often expressed in percentage. This compensation level is usually measured with respect to the transmission line reactance. For example, we shall refer the compensation level as 50% when λ = X /2. In the analysis presented below, we assume that the injected voltage lags the line current. The implication of the voltage leading the current will be discussed later.

Applying KVL we get

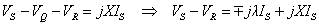
Assuming V_S = V < δ and V_R = V <0° , we get the following expression for the line current

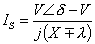(10.21)

When we choose V_Q = λ I_S e^{- j90°} , the line current equation becomes

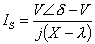
Thus we see that λ is subtracted from X . This choice of the sign corresponds to the voltage source acting as a pure capacitor. Hence we call this as the capacitive mode of operation . In contrast, if we choose V_Q = λI_S e^+j90° , λ is added to X , and this mode is referred to as the inductive mode of operation . Since this voltage injection using (10.20) add λ to or subtract λ from the line reactance, we shall refer it as voltage injection in constant reactance mode. We shall consider the implication of series voltage injection on the transmission line voltage through the following example.

Example 10.3