Inductance of Three-Phase Lines with Symmetrical Spacing

Consider the three-phase line shown in Fig. 1.6. Each of the conductors has a radius of r and their centers form an equilateral triangle with a distance D between them. Assuming that the currents are balanced, we have

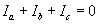(1.23)

Consider a point P external to the conductors. The distance of the point from the phases a, b and c are denoted by D_pa, D_pband D_pcrespectively.

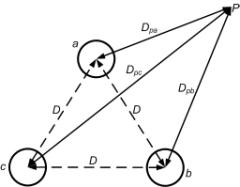
Fig. 1.6 Three-phase symmetrically spaced conductors and an external point P.

Let us assume that the flux linked by the conductor of phase-a due to a current I_a includes the internal flux linkages but excludes the flux linkages beyond the point P . Then from (1.18) we get

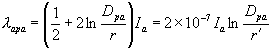(1.24)

The flux linkage with the conductor of phase-a due to the current I_b , excluding all flux beyond the point P , is given by (1.17) as

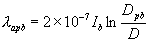(1.25)

Similarly the flux due to the current I_c is

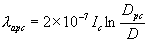(1.26)

Therefore the total flux in the phase-a conductor is

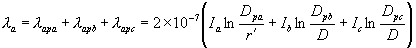
The above expression can be expanded as

(1.27)

From (1.22) we get

Substituting the above expression in (1.27) we get

(1.28)

Now if we move the point P far away, then we can approximate D_pa » D_pb » D_pc.. Therefore their logarithmic ratios will vanish and we can write (1.28) as

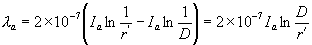(1.29)

Hence the inductance of phase-a is given as

(1.30)

Note that due to symmetry, the inductances of phases b and c will be the same as that of phase-a given above, i.e., L_b= L_c = L a .