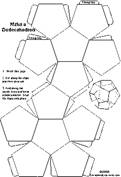
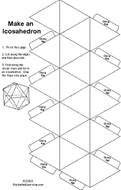
Plate 14 A Decahedrons		14 B Icosahedrons
			Number of faces: 20
			Number of edges: 30
		Number of vertices: 12

(Source : http://www.google.co.in/#hl=en&output=search&sclient=psyab&q=Icosahedron&oq=Ico
sahedron&gs_l=hp.12...18889.18889.0.22250.1.1.0.0.0.0.0.0..0.0...0.0...1c.Wnow7ZKiUR8&pbx=
1&bav=on.2,or.r_gc.r_pw.r_qf.,cf.osb&fp=cfdc15839f96c02&biw=1328&bih=574 ; July 30, 2012)

Exercise #4 & 5 Make the above structure by cutting from the above diagram in card-board

The Platonic Solids are just the beginning of a vast range of convex and compound polyhedron (a solid figure bounded by plane polygons or faces). The application of polyhedron in models and even buildings, from the Neolithic times to the present is available through human history. Leonardo da Vinci, Albert Dürer, M. C. Escher, and Buckminster Fuller are among the many artist- designers and architects captivated by the polyhedral forms and their uses. This makes the components easily mass-producible. Buckminster Fuller argued to promoting his Geodesic Dom structures and buildings. It has also proven valuable in making sphere-approximating objects such as, soccer balls, out of materials like leather. Each polygonal plane (cut out from leather) is connected to other to develop the shape of a sphere.  
(Read more: http://www.dartmouth.edu/~matc/math5.geometry/unit6/unit6.html ; July 30, 2012)