2-dimensional array

. storage can be either row major or column major

. in case of 2-D array stored in row major form address of A[i₁ , i₂ ] can be calculated as

base + ((i₁ - low ₁ ) x n₂ + i₂ - low ₂ ) x w

where n ₂ = high₂ - low₂ + 1

. rewriting the expression gives

((i₁ x n ₂ ) + i ₂ ) x w + (base - ((low ₁ x n₂ ) + low ₂ ) x w)

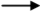((i₁ x n₂ ) + i₂ ) x w + constant

. this can be generalized for A[i₁ , i₂ ,., i_k ]

Similarly, for a row major two dimensional array the address of A[i][j] can be calculated by the formula :

base + ((i-low_i )*n2 +j - low_j )*w where low _i and low_j are lower values of I and j and n2 is number of values j can take i.e. n2 = high2 - low2 + 1.

This can again be written as :

((i * n2) + j) *w + (base - ((low_i *n2) + low_j ) * w) and the second term can be calculated at compile time.

In the same manner, the expression for the location of an element in column major two-dimensional array can be obtained. This addressing can be generalized to multidimensional arrays.