|
Rules for Symbol Table entry
D 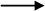 id : T id : T |
addtype(id.entry, T.type)
|
T 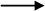 char char |
T.type = char
|
T 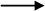 integer integer |
T.type = int
|
T 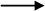 ^T1 ^T1 |
T.type = pointer(T1 .type) |
T 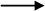 array [ num ] of T 1 array [ num ] of T 1 |
T.type = array(1..num, T 1 .type)
|
Type checking of functions
E 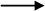 E1 ( E2 ) E1 ( E2 ) |
E. type = if E2 .type == s and
E1 .type == s 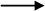 t t
then t
else type-error
|
| |
| |
| |
The rules for the symbol table entry are specified above. These are basically the way in which the symbol table entries corresponding to the productions are done. Type checking of functions
The production E -> E ( E ) where an expression is the application of one expression to another can be used to represent the application of a function to an argument. The rule for checking the type of a function application is
E -> E1 ( E2 ) { E.type := if E2.type == s and E1. type == s -> t then t else type_error }
This rule says that in an expression formed by applying E1 to E2, the type of E1 must be a function s -> t from the type s of E2 to some range type t ; the type of E1 ( E2 ) is t . The above rule can be generalized to functions with more than one argument byconstructing a product type consisting of the arguments. Thus n arguments of type T1 , T2
... Tn can be viewed as a single argument of the type T1 X T2 ... X Tn . For example,
root : ( real real) X real real
declares a function root that takes a function from reals to reals and a real as arguments and returns a real. The Pascal-like syntax for this declaration is
function root ( function f (real) : real; x: real ) : real
|