| L attributed definitions .
. A syntax directed definition is L-attributed if each inherited attribute of X j (1 = j = n) as the right hand side of
A 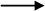 X1 X 2 .Xn depends only on X1 X 2 .Xn depends only on
- Attributes of symbols X1 X 2 .X j-1 and
- Inherited attribute of A
. Consider translation scheme
A 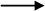 LM LM |
L.i = f1 (A.i)
|
| |
M.i = f2 (L.s)
|
| |
As = f 3 (M.s)
|
A 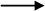 QR QR |
Ri = f 4 (A.i) |
| |
Qi = f 5 (R.s)
|
| |
A.s = f6 (Q.s)
|
We assume that we have inherited attributes, which means that attribute of a symbol will be defined in terms of its sibling and its parent node. Suppose for the production A -> XYZ, if we have to write a function of Yi . Yi can be a function of, in general, of A inherited attribute of X and attribute of Y. However, no matter what parsing we use (top-down or bottom up) we won't be able to evaluate Y in a single pass, as we can never have Z evaluated till then. Clearly, the general definition of attribute equation doesn't work. We, therefore have to modify the attribute equation, in
effect limit it.
This further restriction is such that we can evaluate a function in a left-first traversal order . To achieve this Yi should be a function of A (inherited) and X (inherited and synthesized). The generalization of this rule is that inherited attribute of X will depend only on its left sibling and not on its right sibling. Note that we cannot use the synthesized attribute
of the parent, because these, in general, will be a function of all X, Y and Z. By this limitation, we can (in both top-down and bottom-up parsing) evaluate the tree as we parse it in a single pass. In the two examples, the first has all functions which satisfy the conditions of L-attributed definitions, but in the second one the second function is using synthesized
attribute of R, this violates the rule that we look only at left sibling, hence the second example is not an L-attributed definition.
|