Recursive descent parsing

First set:

Let there be a production

A α

then First( α ) is the set of tokens that appear as the first token in the strings generated from α

For example :

First(simple) = {integer, char, num}

First(num dotdot num) = {num}

Recursive descent parsing is a top down method of syntax analysis in which a set of recursive procedures are executed to process the input. A procedure is associated with each non-terminal of the grammar. Thus, a recursive descent parser is a top-down parser built from a set of mutually-recursive procedures or a non-recursive equivalent where each such procedure usually implements one of the production rules of the grammar.

For example, consider the grammar,

type simple | 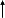id | array [simple] of type

simple integer | char | num dot dot num

First ( a ) is the set of terminals that begin the strings derived from a . If a derives e then e too is in First ( a ). This set is called the first set of the symbol a . Therefore,

First (simple) = {integer, char , num}

First (num dot dot num) = {num}

First (type) = {integer, char, num, , array}