| Dimensionality |
- Assume there are k vectors
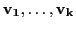
|
- What is their dimensionality?
|
- Vectors
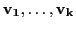 are linearly independent iff the linear combination are linearly independent iff the linear combination 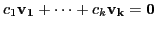 only when only when 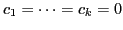
|
- The span of a set of vectors is the vector space generated by their linear combinations
|
- A basis of a vector space
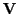 is a set of vectors that are linearly independent and that spans is a set of vectors that are linearly independent and that spans 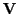
|
- The cardinality of the basis of a vector space
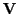 , i.e., the number of linearly independent vectors needed to span , i.e., the number of linearly independent vectors needed to span 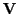 is called its dimensionality is called its dimensionality
|
- The bases (i.e., the basis vectors) may vary, but their cardinality remains the same
|