| |
| kNN query |
- 1-NN query of
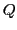 has true answer has true answer 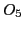
|
- Applying 1-NN on l projections gives l collision sets:
|
| |
- 2,9,13:
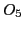
|
| |
- 7,10,14:
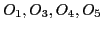
|
| |
- 1,5,11:
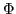
|
| |
- 8,12,14:
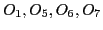
|
- Now majority counting gives
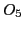
|
- No guarantee of correct answer
|
- Accuracy increases with more runs
|
- It can be proved that
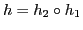 is approximately distance preserving provided is approximately distance preserving provided 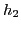 is so ( is so (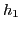 already is so!) already is so!)
|
- Therefore, this is a Monte Carlo algorithm
|
- Time:
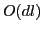 where where 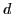 is the dimensionality (here, 3) is the dimensionality (here, 3)
|
- Extensions for Euclidean space: E2LSH
|
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|