|
Radix Complement :
The r’s complement of an n-digit number in base r is defined as  for N != 0 and 0 for N = 0.
r’s complement is obtained by adding 1 to the ( r - 1 )’s complement, since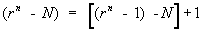 
e.g., 10's complement of 5642 is 9's complement of 5642 + 1, i.e., 4357 + 1 = 4358
e.g., 2's complement of 1010 is 1's complement of 1010 + 1, i.e., 0101 + 1 = 0110.
Representation of Signed integer in 1's complement form:
|
Consider the eight bit number 01011100, 1's complements of this number is 10100011. If we perform the following addition:
If we add 1 to the number, the result is 100000000.
|
|
|
0 1 0 1 1 1 0 0
|
|
1 0 1 0 0 0 1 1
|
|
----------------------------
|
|
|
|
Since we are considering an eight bit number, so the 9th bit (MSB) of the result can not be stored. Therefore, the final result is 00000000.
Since the addition of two number is 0, so one can be treated as the negative of the other number. So, 1's complement can be used to represent negative number.
|